|
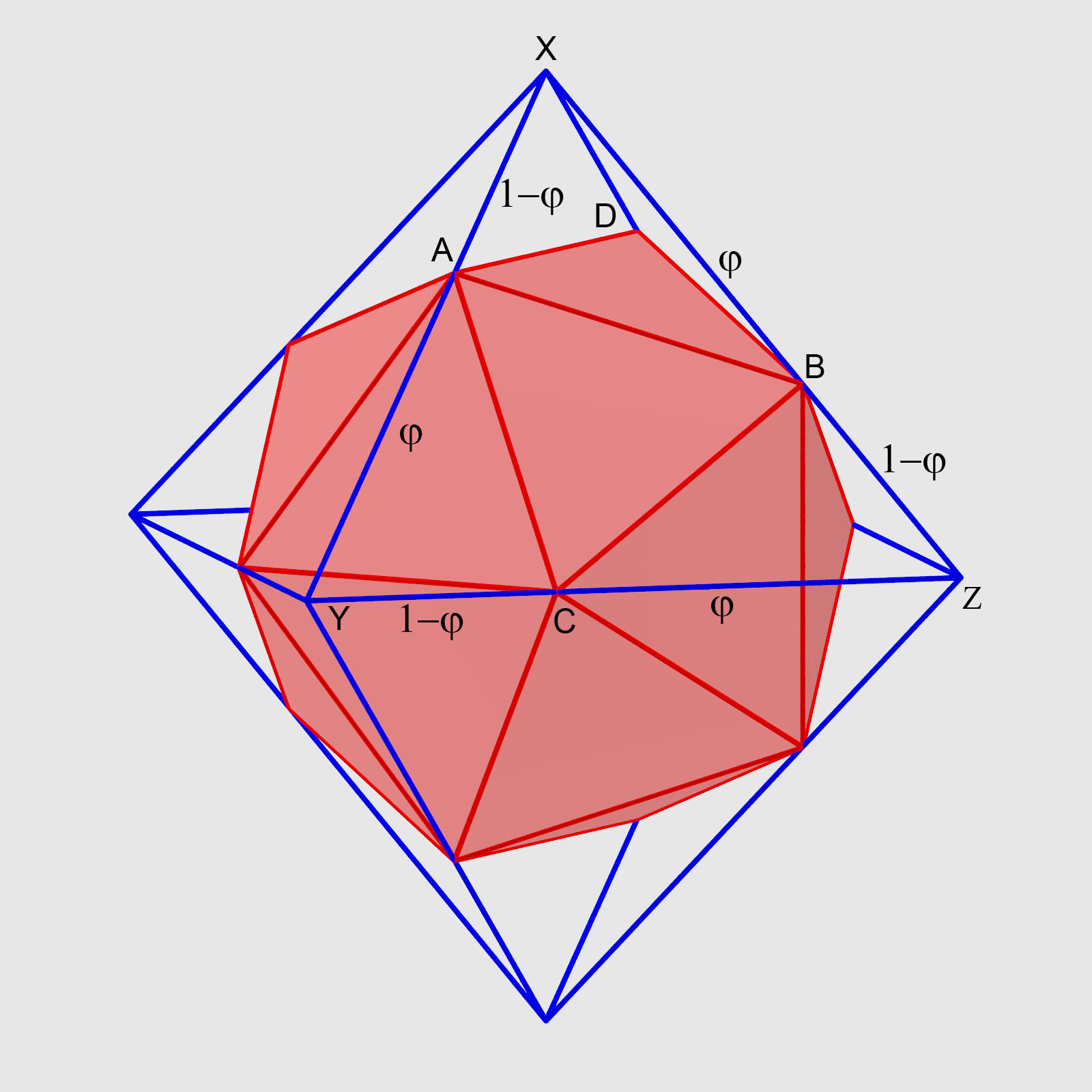
Inscribing a regular icosahedron into a regular octahedron
Dividing the edges of a regular octahedron in an appropriate way the 12 division points are the vertices of a regular isosahedron. To obtain this result the division points should be determined using the "golden section".
If we suppose the length of the edges of the regular octahedron is 1, the length of the segments on each edge are $\varphi = \dfrac{\sqrt{5}-1}{2}$ and $1-\varphi = \dfrac{3-\sqrt{5}}{2}$.
It is well known that $1-\varphi = \varphi^2$.
More about the golden section: Golden section - Golden Triangle - Pentagon and Pentagram - Dodecahedron (update: november 2025)

|
We have to prove that all the faces of the icosahedron are equilateral triangles.
The 8 faces of the icosahedron located in the faces of the regular octahedron are equilateral triangles. The length of the side can be calculated using the cosine rule in a triangle such as ABX.
$$AB^2=AX^2+XB^2-2 AX.XB.\cos \widehat{AXB}$$
As $AX=1-\varphi = \varphi^2$, $XB=\varphi$ and $\widehat{AXB} = 60^\circ$, we get:
$$AB^2=\varphi^4+\varphi^2-2 \varphi^2.\varphi.\frac{1}{2}$$
$$AB^2=\varphi^4+\varphi^2.(1-\varphi) = 2 \varphi^4$$
$$AB = \sqrt{2}\varphi^2 = \sqrt{2}(1-\varphi)$$
Now we prove that the other 12 faces of the icosahedron, such as AXD also are equilateral triangles!
As $\widehat{AXD}=90^\circ$ and $AX=DX=1-\varphi = \varphi^2$ it follows that
$$AD^2=\varphi^4 + \varphi^4 = 2 \varphi^4$$
$$AD = \sqrt{2}\varphi^2 = \sqrt{2}(1-\varphi)$$.
The icosahedron inscribed in the octahedron is regular. Starting with an octahedron with length of the edges being l he length of all segments should be multiplied by l .
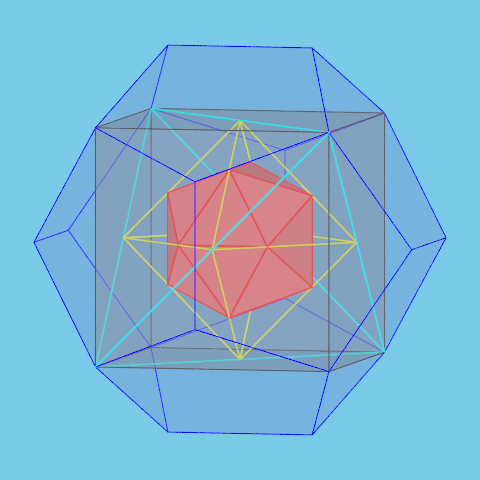
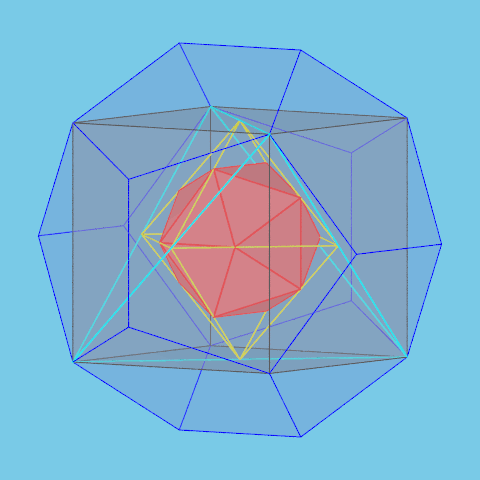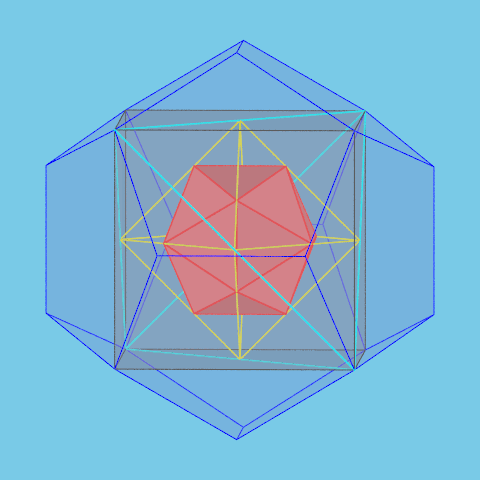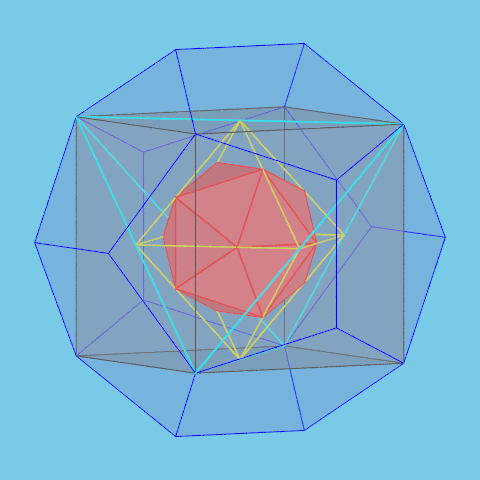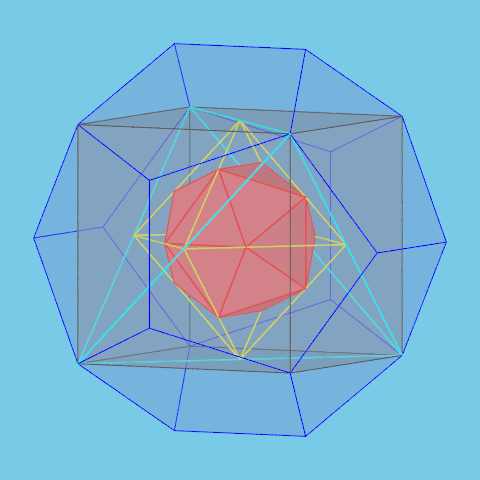
In Plato's dialogue Timaeus the four elements fire, earth, air and water respectively are associated with the tetrahedron, the hexahedron (cube), the octahedron and the icosahedron. The dodecahedron represents the
whole universe (the cosmos).
So it's nice to represent symbolically the four polyhedra representing the elements inside a dodecahedron representing the cosmos.
Eight of the vertices of a regular dodecahedron are the vertices of a cube. In this cube we inscribe a regular tetrahedron. The midpoints of the edges of this tetrahedron are the vertices of
a regular octahedron. Finally, in this octahedron we construct a regular icosahedron using the method explained before.
If the length of the edge of the dodecahedron is 1, the length of the edges of the cube, the tetrahedron, the octahedron and the icosahedron respectively are
$\dfrac{1}{\varphi}$, $\dfrac{\sqrt{2}}{\varphi}$, $\dfrac{1}{\varphi \sqrt{2}}$ and $\varphi$.
|
|
return to the homepage
Send an e-mail
Last update: November 2025.