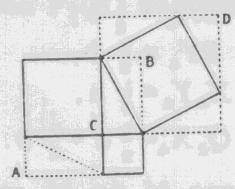
529. Ik vond onlangs een nieuw bewys voor de stelling van PYTHAGORAS. Hier is het. Door, als op nevenstaand voorbeeld, zes driehoeken te construeeren - ieder gelyk aan den gegeven rechthoekigen driehoek - verkrygt men twee gelyke kwadraten, AB en CD. *) Als men van elk dezer figuren vier driehoeken aftrekt, bewyst de gelykheid van 't overschot aan weerszy, wat er te bewyzen was.

Eenvoudiger kan het niet, dunkt me. Na dit bewys gevonden te hebben, vernam ik dat er een werkje bestond, waarin dit onderwerp werd behandeld. Ik schafte my dat boekje aan **) en vond er myn demonstratie niet in. Ook meen ik dat geen der daarin voorkomende bewyzen zoo aanschouwelyk en helder is als 't myne. Wie beweeren mocht dat het reeds vroeger was gevonden, zou me verplichten met de opgave waar het gepubliceerd is ? ***) Professor HOFMANN kende 't niet, en ook STROOTMAN zou er wel melding van gemaakt hebben, als 't hem bekend ware geweest. HOFMANN schynt een speciale studie te hebben gemaakt zoowel van de propositie zelve, als van de litteratuur over dit onderwerp.

Ik hoop dat niemand vragen zal welk nut het heeft, te zoeken naar eenvoudiger bewyzen voor 'n bekende waarheid? Dit streven leidt tot helderheid van opvatting, en gewent ons aan duidelyke voorstelling. ,,Bien poser une question, c'est presque la résoudre.'' Dit geldt zoowel in menschkunde, moraal, politiek, enz. als in de eigenlyk gezegde wiskunde. De natuur kent al die onderscheidingen niet. Zy streeft - onbewust - met één middel naar één doel, en er is verband tusschen de helderheid van myn bewys voor de stelling van PYTHAGORAS, en de eenvoudigheid der geloofsbelydenis die ik neerlegde in de vertelling over LYSTERMANNETJE.

De leerlingachtige verdeeling in verschillende soort van kunden, in logiën, is 'n gevolg onzer kleinheid, die niet in-staat is, alles te-gelyk te omvatten. Wy ontleden waar de Natuur samenvat, en spellen wat zy schryft. (491) Nu, schande is 't niet, dat wy door spellen tot lezen moeten komen. Maar 't is van belang, te onthouden dat ons spellen geen lezen is.

*) Volgens het postulaat, zyn de zyden onderling gelyk, en de hoeken recht. Dat de figuren AB en CD inderdaad vier zyden hebben, en niet meer, wordt hieruit bewezen, dat overäl de tegen die zyden aanliggende hoeken twee rechte uitmaken. (1865)

**) De 47e Propositie van EUCLIDES, door J.J.I. HOFMANN, hoogleeraar in de wiskunde te Aschaffenburg, vertaald door H. STROOTMAN, lector in de wiskunde, aan de militaire akademie te BREDA. (1865)

***) Niemand heeft my de prioriteit betwist. (1872)

De stelling van Pythagoras is dat in een rechthoekige driehoek het kwadraat van de lengte van de zijde die niet eindigt in de rechte hoek gelijk is aan de som van de kwadraten van de lengten van de zijden die wel eindigen in de rechte hoek.

Deze stelling werd voor 't eerst tussen -600 en -500 gevonden, en heeft een bewijs in 't eerste boek van Euclides, dat van ca. -300 dateert, en de toen bekende meetkunde axiomatisch en logisch in kaart bracht.

't Belang van de stelling ligt 'm vooral in 't feit dat men er de afstand tussen 2 punten kan vinden die men niet empirisch kan meten, door een constructie als van Pythagoras op te zetten waarin deze afstand als de diagonaal in een rechthoekige driehoek functioneert, en waarvan de zijden die aan de rechte hoek raken empirisch wel makkelijk meetbaar zijn.

Voor de liefhebbers is er een fraai en geloofwardig verhaal van de filosoof Thomas Hobbes, over hoe hij reageerde op 't lezen van deze stelling in Euclides, en een fraai en ongeloofwaardig verhaal van de zuster van Blaise Pascal, hoe Blaise als kind de eerste stellingen van Euclides zelfstandig vond en bewees, in de volgorde waarin Euclides dat gedaan had. ('t Ongeloofwaardige schuilt vooral in deze laatste toevoeging, en niet in de geheel terechte suggestie dat Pascal een wiskundig genie was.)

Wat betreft: "Eenvoudiger kan het niet, dunkt me": Toch wel. 't Allerfraaiste bewijs is van de hand van de Chinezen, als ik 't wel heb uit het jaar 200.

Hier is 't. Konstrueer een vierkant ABCD, en neem op één van de zijden, bijvoorbeeld AB, een lijnstuk E en pas dat af op alle zijden. Verbindt de vier gevonden punten. Je krijgt een figuur als deze:

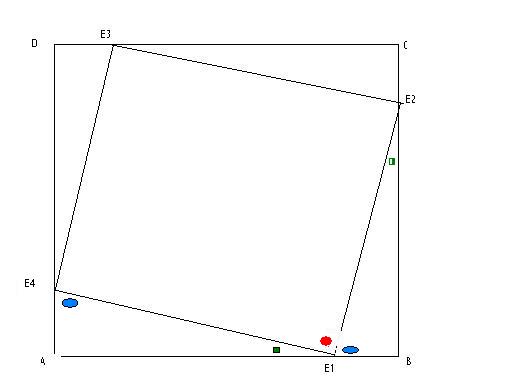
Laten we eerst bewijzen dat de ingesloten hoek E1 aangegeven met een rode cirkel 90° is. Deze hoek is samen met de twee die eraan grenzen - aangegeven met groen vierkant en blauwe ellips - 180°. Maar A en B vormen rechte hoeken (zijn immers de hoeken in een vierkant) en de twee driehoeken zijn gelijk (met twee gelijke zijden en een gelijke daardoor gevormde - rechte - hoek). Aangezien de som van de hoeken in een driehoek 180° is volgt dat de hoeken aangegeven met groen vierkant en blauwe ellips   samen 90° zijn, waaruit volgt dat de resterende ingesloten hoek gelijk 90° is. Dus de ingesloten figuur is ook een vierkant, want de zijden zijn allen gelijk en voor alle hoeken geldt hetzelfde argument.

Maar nu geldt het volgende eenvoudige sommetje:

Noem de afstand AE1=a en E1B=d. Dan is het grote kwadraat ABCD = (a+d)^2=a^2+2ad+d^2. Alle vier driehoeken zijn gelijk, en twee samen tegenelkaar gelegd vormen een rechthoek ter grootte van ad. De vier driehoeken samen zijn dus 2ad groot. Indien we dit aftrekken van ABCD houden we het kleine kwadraat over dat daarmee gelijk is aan de som der kwadraten van de twee zijden die de rechte hoek vormen in ieder der vier driehoeken. Qed. 

En wat betreft: "Wie beweeren mocht dat het reeds vroeger was gevonden, zou me verplichten met de opgave waar het gepubliceerd is?" Ik heb begrepen dat 'tzelfde bewijs in 1832 gepubliceerd is door een Engelse wiskundige. Dit betekent niet dat Multatuli 't niet zelf vond, en ook vermindert het zijn prestatie niet: Immers, er zijn veel bewijzen voor gezocht en gevonden door de eeuwen heen, omdat de stelling van zo fundamenteel belang is, en het bewijs van Euclides bepaald niet het inzichtelijkste is dat gegeven zou kunnen worden.

In ieder geval is 't een interessant feit over de hele Westerse wiskunde dat het inderdaad niet te verbeteren Chinese bewijs voor de stelling van Pythagoras bij mijn weten nooit gevonden is in 't Westen, ondanks veel moeite.

Tenslotte moet ik iets toevoegen over.... Neerlandici en wiskunde:

Het geval wil dat het meest informatieve boek in één band over Multatuli K. ter Laan's Multatuli Encyclopedie is. Het geeft namelijk achtergrondsinformatie bij tal van namen en frasen die M. gebruikt in zijn gepubliceerd werk. Dit verheldert veel, want Multatuli gebruikt veel verwijzingen en ongebruikelijke termen. Kornelis ter Laan was 'de eerste rode burgemeester van Zaandam' en leefde van 1871-1963 en de Multatuli Encyclopedie is voor een groot deel zijn werk.

Maar hij slaagde er niet in e.e.a. gepubliceerd te krijgen, en uiteindelijk is zijn werk na zijn dood uitgegeven door een comité van Gediplomeerde Neerlandici met steun van "de gelden van het Prins Bernhard Fonds", want moderne gediplomeerde Neerlandici plegen hun nuttige werken alleen voor Staats-subsidies te verrichten en onder leiding van Begeleidingscommissies.

Deze hooggeleerde Begeleidingscommissie - ik tel in één alinea drie Neerlandistieke professor doctoren; twee idem doctoren; en twee doctorandussen - streefde ernaar hun bewerking van K. ter Laan's Multatuli Encyclopedie uit te geven in het jaar 1987, waarin M. honderd jaar dood was. Zoals ook gebeurde met de uitgave van de VW - 25 delen in 50 jaren gesubsidieerde Neerlandistieke arbeid - nam de uitgave ietsje langer dan begroot: Uiteindelijk zag het werk het licht in 1995 met steun van het Prins Bernhardfonds, het ministerie van WVC, het Cultuurfonds van het Bouwfonds der Nederlandse Gemeenten, de gemeente Zaanstad, de Maatschappij der Nederlandse Letterkunde e.a. subsidiegevers.

Wat leert dit eminente gezelschap van Neerlandistieke geleerden onder beheer van zwaar academisch getitelde Begeleidingscommissies en gesubsidieerd door een groot deel der Nederlandse subsidiegevers nu over ... de stelling van Pythagoras, ondertussen 25 eeuwen oud en - ooit - onderwezen aan ALLE Neerlandistieke hooggeleerden?

Bereid u voor paf te staan in amechtige bewondering, lezer!

" Pythagoras, ca. 570-500 v.Chr., beroemd Grieks wijsgeer en wiskundige. zijn naam werd vereenvoudigd door het naar hem genoemde theorema van de wiskunde: de stelling van Pythagoras (a²=b²=c²) "

Ja, deze volmaakte onzin staat er écht - en uit de rest van het artikel (noch de hele Encyclopedie) blijkt geen enkel begrip voor wiskunde, zelfs niet de allerelementairste.

I rest my case.