Normally a billiards game is played on a rectangular table. On a "mathematical billiard table" we consider only one ball. Moreover, this ball is reduced to a point that moves in a straight line until it hits an edge and bounces back in such a way that the angle of reflection equals the angle of incidence. Both angles can be considered as the angles formed by the side of the table involved and the incoming and outgoing lines. The mathematician Charles L. Dodgson, better known as Lewis Carroll, the author of "Alice in Wonderland" thought and wrote about circular billiard tables.

We'll consider a billiard table that takes the shape of an ellipse. I started this page in 2002, but only in 2007 I discovered the book Geometry and Billiards by Serge Tabachnikov. In this book (186 pages) the author treats different billiard table shapes and the (often not so elementary) mathematics behind them. The bouncing law is linked to the reflection law in optics. As to elliptical billiards this leads in a short and elegant way to the property that a shot passing through one focus is reflected through the other focus. A nice geometrical proof of this property is mentioned further. The book also contains an extensive bibliography.

The animations on this page have been made using Maple.

First we remind some facts about ellipses.

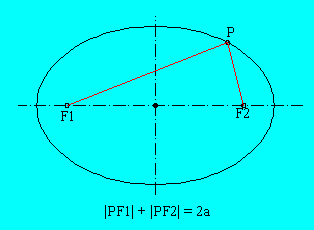
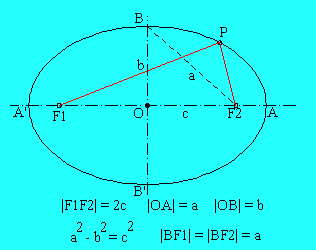
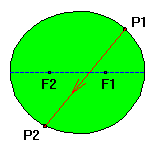
Given two fixed point F1 and F2 in a plane, an ellipse is the locus of all points P in that plane for which the sum of the distances to F1 and F2 equals a given value 2a.
The given points F1 and F2 are called the foci or focal points of the ellipse, PF1 and PF2 are called the focal radii of the point P.
For all points outside the ellipse the sum of the distances to the focal points is larger than 2a, for all points inside the ellipse it is smaller than 2a.

Given the value 2a and calling 2c the distance between the foci F1 and F2 we are easily led to the length of the axes of the ellipse. The length of the major axis AA' is 2a and the length of the minor axis BB' is 2b. The relation between a, b and c is illustrated on the next picture.




The property that will be most useful in the further treatment of our subject is illustrated on the next picture: for any point P on the ellipse, the bisectors b and b'of FP and F'P are the tangent and normal in P to the ellipse.

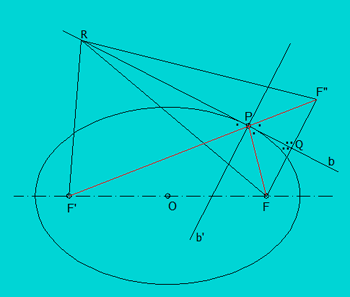
The orthogonal line from F to b meets b in Q and F'P in F". For any point R (different from P) on b we have: RF = RF". Furthermore RF'+ RF" > F'F" = F'P + PF = 2a.

From the definition of the ellipse it follows that R is outside of the ellipse, and so are all points on b different from P. This means that the bisectors b and n are the tangent and normal in P to the ellipse.

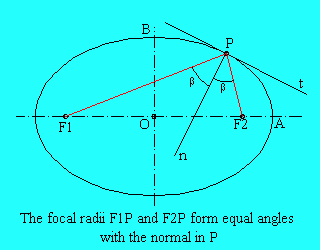
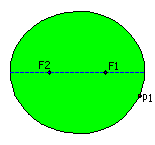
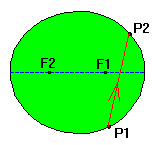
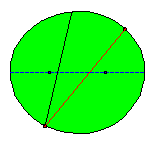
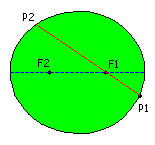
The ball is positioned in P1 and shot in the direction of the focus F1. If the ball hits the border of the table in P2 it will be be bounced according to the law of reflection: the angle between the incoming path and the normal in P2 equals the angle between this normal and the outgoing path. As a consequence of the property last mentioned the ball will bounce back along P2F2 !
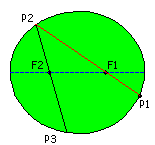
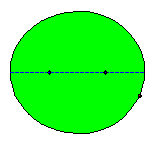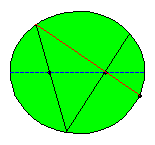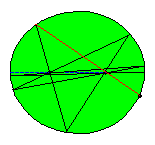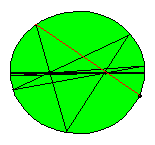
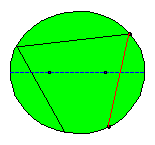
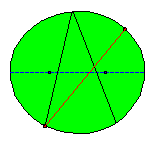
After a new hit the ball will bounce through the other focus F1. In the following illustration we consider a sequence of consecutive bounces.

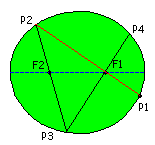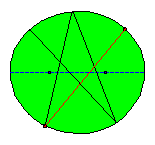
After a rather small number of bounces the ball seems to travel along the major axis!

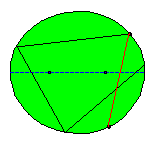
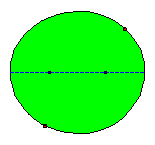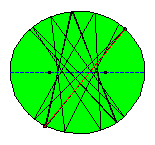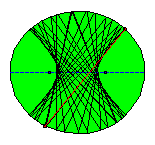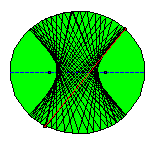
If the first shot doesn't pass over a focus none of all subsequent reflected paths will pass over a focus. But also in this case the mathematical elliptical billiard game leads to interesting patterns!

General situation

It follows from the mentioned property of the focal radii in relation with the normal or tangent in the reflection point that none of all subsequent reflected segments will pass between the foci of the ellipse. If we consider a large number of reflected segments there seems to arise a new ellipse! Some knowledge of calculus is needed to find out that this curve, known as the evolute of the reflected segments indeed is an ellipse and moreover the foci of this ellipse are the same as those of the original ellipse!

In Tabachnikovs book one can find a proof of the property that (in general) a billiard trajectory inside an ellipse remains tangent to a confocal conic.

In the following animated picture 50 reflections are shown.

Some exceptions: periodical paths.

One easily can see that there exist particular situations: in some cases the paths are periodical and don't lead to a new ellipse inside the given one. We give two examples: a quadrangular path and a hexagonal path.

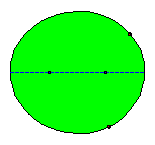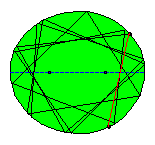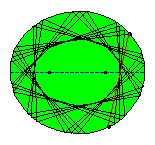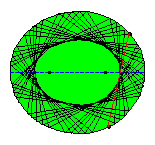
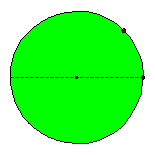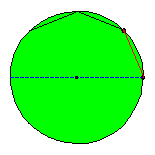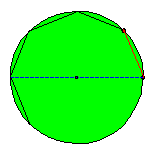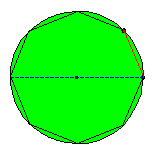
The circle as a special ellipse.

A circle can be considered as a special ellipse: the foci F1 and F2 coincide, a = b = radius circle ; c = 0. If a path is non periodical the evolute of the reflected shots is a new circle with the same centre. Perhaps the existence of periodical paths is more easy to be seen.

Second case: the first shot passes between the foci of the ellipse.

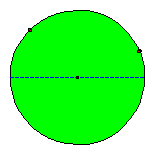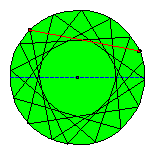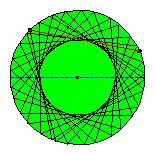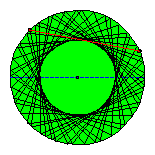General situation

It follows from the mentioned property of the focal radii in relation with the normal or tangent in the reflection point that all subsequent reflected segments will pass between the foci of the ellipse. If we consider a large number of reflected segments there seems to arise a new curve! Some knowledge of calculus is needed to find out that this curve, known as the evolute of the reflected segments is a hyperbola and moreover the foci of this hyperbola are the same as those of the original ellipse!
The definition of a hyperbola resembles the definition of an ellipse: given two fixed point F1 and F2 in a plane, a hyperbola is the locus of all points P in that plane for which the difference of the distances to F1 and F2 equals a given value 2a. The given points F1 and F2 are called the foci of the hyperbola and PF1 and PF2 are called the focal radii of the point P.

In the following animated picture 50 reflections are shown.

Also in this case one can imagine that exceptions exist. An example: if we push the ball along the minor axis of the ellipse it will continuously bounce along the same axis.

---

Herman Serras, Last updated February 2018
return to the homepage