The Golden Section
The Golden Triangle
The Regular Pentagon and the Pentagram
The Dodecahedron



On this page we will derive some relations between a fundamental number and two famous geometrical figures, the one planar, the other spatial. As a result we will understand how a regular dodecahedron can be constructed starting from a cube by putting suitable "roofs" on it, as Euclid already did...

The Golden Section



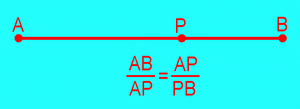
The starting point is the division of a line segment in mean and extreme ratio.
A point on a line segment divides this segment in mean and extreme ratio if the ratio of the whole segment to one part is the same as the ratio of that part to the remaining part of the line segment.
Given a line segment AB, the point P divides AB in mean and extreme ratio if

AB/AP = AP/PB

This division of the line segment is called the golden section. The ratio AB/AP is called the golden number and often represented by the greek character capital PHI.

A special isosceles triangle or "golden triangle"



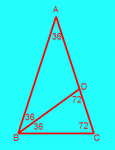
We consider an isosceles triangle with a top angle measuring 36 degrees. Both base angles then measure 72 degrees. BD is the bisector of the angle in B.
From the fact that the triangles ABD and BDC are isosceles triangles it follows that

BC=BD=AD.

Moreover the triangles BDC and ABC are similar triangles. It follows that

AC/BD = BC/DC or AC/AD = AD/DC,

which means that in the original triangle the base BC equals the greatest part of the side AC divided by the golden section!

If we consider the circle with centre A and radius AB, then BC is a side of the regular decagon that is inscribed in the given circle.

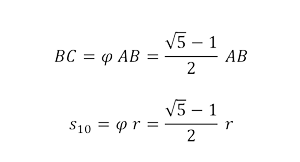
A property of the regular pentagon

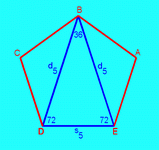
Considering a regular pentagon with two non-intersecting diagonals and taking into account what we already derived above, it follows that the length of the side equals the greatest part of the diagonal divided by the golden section.

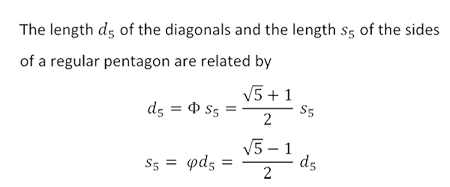
The pentagram

The five diagonals of a regular pentagon define a star-shaped figure that is called a pentagram . It has five sides and five vertices. The interior intersections of the sides aren't vertices of the pentagram. A pentagram is an example of a non-convex polygon. A polygon is convex if and only if any line containing a side of the polygon doesn't contain a point in the interior of the polygon. As a triangle always is convex and there don't exist non-convex regular polygons with four sides, the pentagram, in this sense is the simplest of the non-convex regular polygons.
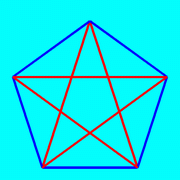
From the relation between the sides and the diagonals of a regular pentagon and considering the the second figure above, one easily states that two non-consecutive sides of a pentagram divide each other in mean and extreme ratio!

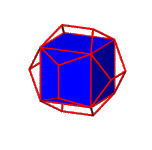
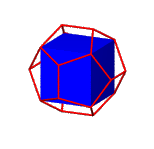
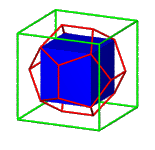
Construction of a regular dodecahedron

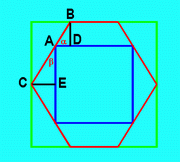
Starting with a cube we can construct a regular dodecahedron by putting appropriate "roofs" on each face of the cube. This is the method used by Euclid (book XIII proposition 17). The bases of the roofs are the faces of the cube and all edges of the roofs that aren't edges of the cube must have the same length. Moreover the adjacent faces of two meeting roofs must form a regular planar pentagon. The length of the diagonals of the pentagons equals the length of the sides of the cube. It follows that the length of the edges of the dodecahedron is the greatest of the two parts in which the edge of the cube is divided by the golden section!
The height of the roofs equals half the side of the pentagons.

As easily can be derived from a frontal view, the angles between the base and a triangular face and between the base and a trapeziodal face of the roof are complementary. It follows that the pentagons are planar.

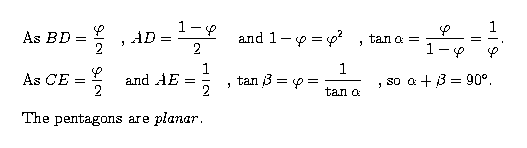
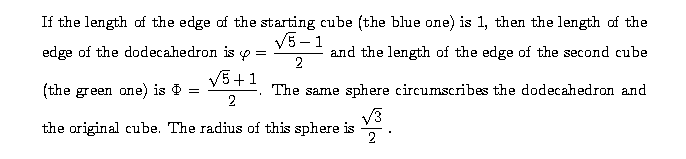
A cube-to-dodecahedron transformation
Bob Faulkner informed me via email from America how he had constructed a material model to illustrate a nice cube-to-dodecahedron transformation. Complimenting me on my own displays, he asked if I might realize his material model as a computer animation. I accomplished the animation by following Euclid's method: first defining six roofs upon a given cube, then completing the roofs by including their square bases. In this way, the original cube could be omitted. Next, choosing one of the roofs as fixed, the four adjacent roofs were hinged along their edges common with the fixed roof. The sixth roof was then hinged to one of its already hinged neighbours. Finally, it's possible to unfold the dodecahedron and refold it into the cube that served as the basis for its construction. Following Bob's idea, I prepared an endless computer animation to illustrate this very nice relation between the cube and the dodecahedron that's constructed upon it.

return to the homepage