 |
A proof of the Pythagorean theorem using "rearrangement"
The Pythagorean theorem, or Pythagoras' theorem is a relation among the squares constructed on the sides of a right triangle (or right-angled triangle).
In his monumental book "The thirteen books of Euclid's Elements, volume I: Books I-II" (Dover Publications, second edition, 1956), augmented with many mathematical and historical annotations, Thomas L. Heath states proposition I47,
better known as the Pythagorean Theorem as follows:
 |
 |
 |
Hundreds of proofs of the Pyhagorean theorem exist. Some of these proofs use algebraic formulas. Other proofs, such as the original proof of I47 in the Elements, are purely geometrical. They compare areas without using algebraic formulas.
For the proof as it appears in the "Elements" click here
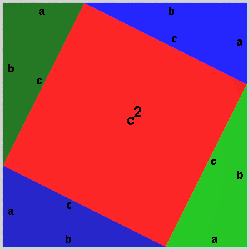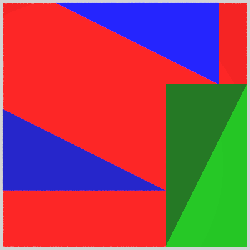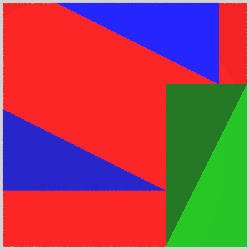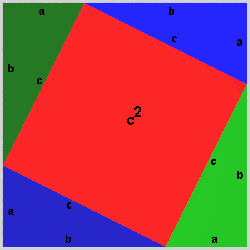
One of the most simple proofs only uses a rearrangement of triangles within a square and the "Common notions". In the following image, the large square on the left consists of the square on the hypothenuse and four times the right triangle, the same large square on the right is composed of the squares on the two other sides of the right triangle and also four times the tight triangles.
Using common notion 3, we see that the the red square on the left equals the two red squares on the right. And that's what Pythagoras' theorem states!
The animation demonstrates the rearrangement of the triangles.

|
 |

|
This approach is purely geometrical. If we allow the use of algebraic expressions for the length of a line segment and the area of a square, it's clear that the Pythagorean theorem for a right triangle with a and b as the lengths of the rectangular sides and c as the length of the hypothenosa is expressed in the well-know algebraic formula:
 |