 |
Polygonal wheels
 |
Did you ever see a car with square wheels that nevertheless rolls smoothly along a rather strange road?
We want to know more about the shape of this road.
A rolling straight line
We start with a horizontal straight line segment through the point A that we suppose as attached to the point O.
We want to determine the shape of the road in such a way that the point O moves on a horizontal line as the
line rolls over the road (without any slipping).
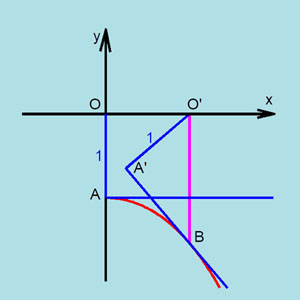 |
Choosing the coordinate system as indicated on the drawing, the equation of the line in the start
position is y = -1 and the origin moves along the x-axis as the line is rolling.
To obtain the equation y = f(x) of the road we express that the length of the curve AB is the same
as the length of the line segment A'B. This yields a differential equation together with the initial condition
f(0) = -1.
The solution of this initial value problem is y = - cosh(x). The function cosh is the
"hyperbolic cosine function" that is linked to the exponential function by the relation
cosh(x) = (exp(x)+exp(-x))/2. The curve represented by the
equation y = cosh(x) is a "catenary", so the "road" we are looking for is an
inverted catenary.
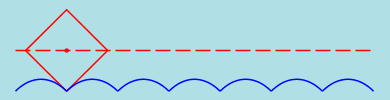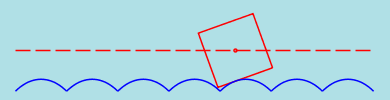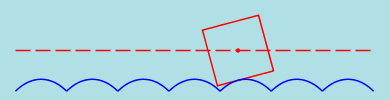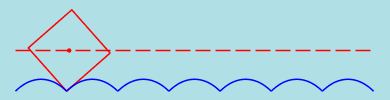
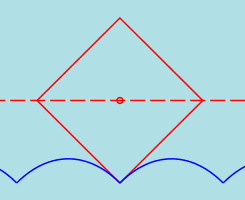
Square wheels
 |
 |
 |
Now we consider a square wheel. It's easy to see that the appropriate road is a sequence of pieces of inverted
catenaries. In the junction points the tangents to both parts of the road must correspond to the angle of
the square as indicated on the figure.
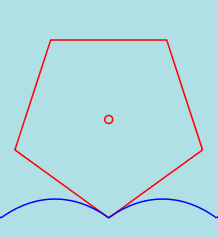
Other polygonal wheels
It's rather easy to consider other wheels that have the form of a regular polygon.
In every case the road consists of a sequence of pieces of inverted catenaries. The angle of the tangents in the
cusps must correspond to the angle of the polygon.
We consider a car with wheels that have the shape of a regular PENTAGON.
 |
 |
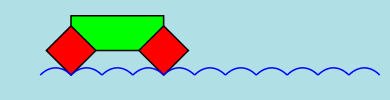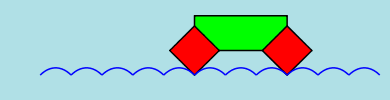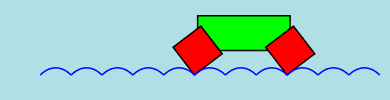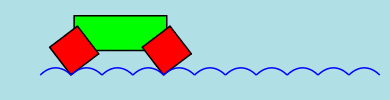
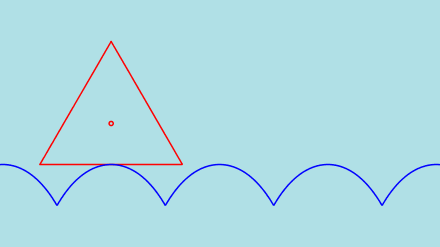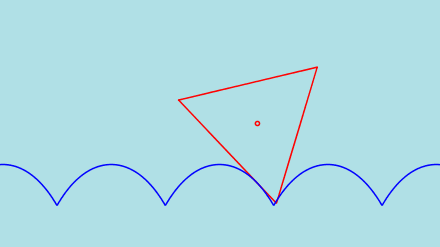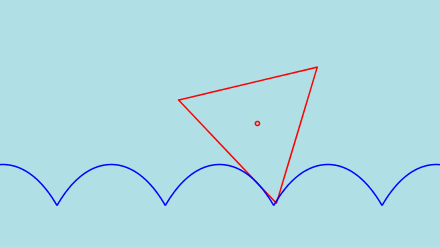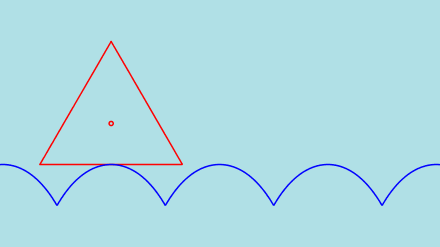
However... an equitriangular wheel will CRASH as can be seen in the following figures. A vertex of the rolling
triangle hits the road before the vertex reaches the cusp.
 |
 |
An interesting (and more general) paper about this subject is "Roads and Wheels" by Leon Hall
and Stan Wagon and published in "Mathematics Magazine", Vol. 65, no 5, december 1992.