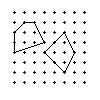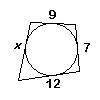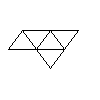Dit is een kopie van een pagina met wiskunde-puzzels die oorspronkelijk te
vinden was op het adres
http://www.molyvos.net/~themini/math_dutch.html.

Plaatjes zijn kloppen nooit precies, en als je het niet kunt laten, dan moet je maar een
rekenmachine gebruiken.
Opgave 1 (10 punten)
Drie personen, meneer Aarts en de heer en mevrouw Bartels, maken een vliegreis.
Iedere passagier mag een bepaald gewicht aan bagage meenemen; voor elke kilogram
meer moet een vastgesteld bedrag extra worden betaald. De bagage van meneer Aarts
weegt 43 kg; die van het echtpaar Bartels weegt ook 43 kg. Meneer Aarts moet,
wegens overwicht, 50 gulden betalen; voor de bagage van meneer Bartels moet 6 gulden
extra worden betaald en voor die van mevrouw Bartels 8 gulden. Hoe zwaar is de
bagage van meneer Bartels?
Opgave 2 (10 punten)
De rij getallen 1,5,4,8,7,11,... ontwikkelt zich volgens het voorschrift: 4 erbij,
1 eraf, 4 erbij, 1 eraf, etc. Het honderdste getal in deze rij is...?
Opgave 3 (10 punten)
In de vermenigvuldiging 17 x 23 = 408 is precies één cijfer verkeerd (typefoutje).
Verbeter de fout.
Opgave 4 (10 punten)
1,2,2,3,3,3,4,4,4,4,5,5,5,5,5,... Wat is het duizendste getal in deze rij?
Opgave 5 (20 punten)
De zes zijvlakken van een kubus denken we ons oneindig voortgezet. De ruimte
wordt door deze vlakken in n delen verdeeld (inclusief het deel binnen de kubus). n = ...?
Opgave 6 (20 punten)
In een (voor de eigenaar winstgevende) geldwisselautomaat moet men òf drie dubbeltjes gooien
òf een kwartje. Voor drie dubbeltjes krijg je één kwartje terug. Voor één kwartje krijg je
twee dubbeltjes. Harm, die de automaat moet testen, begint met 19 kwartjes en 94 dubbeltjes.
Hij wisselt net zo lang geld tot het wisselen niet meer mogelijk is.
Hoeveel munten heeft Harm dan in totaal in de automaat gegooid?
Opgave 7 (10 punten)
Op een groot stijldans-bal zijn 420 personen aanwezig. Op een zeker moment danst 60% van de vrouwen
met 80% van de mannen.
Hoeveel personen zitten er dan aan de kant?
Opgave 8 (10 punten)
Drie hardlopers Jan, René en Thijs houden een wedstrijd over een baan van 400 meter. Ieder loopt
met een constante snelheid. René wint met 50 meter van Thijs (dwz als René over de finish gaat
moet Thijs nog 50 meter afleggen) en Thijs wint met 32 meter van Jan.
Met hoeveel meter wint René van Jan?
Opgave 9 (10 punten)
Een klas krijgt de resultaten van een proefwerk wiskunde terug. De meisjes scoorden gemiddeld 8,5. De
jongens scoorden 7,6 gemiddeld. Het gemiddelde van de totale klas is 8,0. Er zitten 12 meisjes in de klas.
Hoeveel leerlingen telt deze klas?
Opgave 10 (20 punten)
Van een even getal is de som van de cijfers 95; de som van de cijfers van de helft van dat getal is 70.
Hoeveel oneven cijfers heeft dat getal?
Opgave 11 (15 punten)
Van het getal 24865 gaan we cijfers omwisselen. Zo krijgen we 120 verschillende getallen: bijvoorbeeld
24865, 86254 en 42865. Tel al die getallen bij elkaar op. Wat is de uitkomst?
Opgave 12 (20 punten)
Zes mensen (A, B, C, D, E en F) dragen gekleurde petjes. Twee dragen een zwarte, twee een witte en twee mensen
dragen een rode pet. Ze hebben afgesproken dat de mensen met een witte pet altijd de waarheid spreken en dat de
mensen met een zwarte pet altijd liegen. Dragers van een rode pet mogen zelf weten of ze wel of niet liegen. Ze
zitten nu allemaal in een kringetje en doen de volgende uitspraken:
A: "Ik zie precies één wit petje."
B: "Ik zie precies één zwart petje."
C: "Ik zie precies één rood petje."
D: "A draagt een wit petje."
E: "D heeft geen zwart petje."
F: "D heeft geen rood petje."
Niemand ziet zijn eigen petje. Wie dragen de witte, zwarte en rode petjes?
Opgave 13 (20 punten)
In een rij van 1990 reële getallen is elk getal - met uitzondering van het eerste en laatst - gelijk
aan de som van zijn twee buren. De som van de eerste 16 getallen is gelijk aan 18 en de som van de laatste 20
is gelijk aan 24. Bepaal het eerste getal van deze rij.
Opgave 14 (20 punten)
Een rechthoekige foto van 10 bij 15 kan keurig verpakt worden in een rechthoekig stuk papier van
20 bij 15 of 10 bij 30. Er is nog een ander rechthoekig stuk papier te vinden waarin de foto keurig
verpakt kan worden. Geef de maten van die rechthoek.
Opgave 15 (10 punten)
Een rijtje opeenvolgende natuurlijke getallen; het zijn er meer dan twee, maar minder dan tien. Tel je ze bij
elkaar op dan krijg je 65. Wat is het kleinste getal van dit rijtje?
Opgave 16 (10 + 10 punten)
Vijf worpen met een dobbelsteen geven v, w, x, y en z ogen.
a) De kans dat het product vwxyz even is, is .....
b) De kans dat de som v+w+x+y+z even is, is .....
Opgave 17 (15 punten)
Een doos heeft een vierkante bodem van 8 bij 8 cm. Op die bodem liggen vier bollen (elke bol heeft straal 2 cm).
Boven op die vier, in het midden, legt men een vijfde even grote bol. Wat is de afstand van het hoogste punt van
de vijfde pol tot de bodem van de doos?
Opgave 18 (20 punten)
Een kynologenclub telt 40 leden; ze hebben allemaal op zijn minst één hond. Elk van die honden is
een bouvier, een Duitse herder of een retriever.
- 12 leden hebben een bouvier, 22 een Duitse herder en 19 een retriever.
- 8 leden hebben zowel een Duitse herder als een retriever.
- Geen van de leden heeft zowel een bouvier als een retriever.
Hoeveel leden hebben een Duitse herder en geen bouvier en geen retriever?
Opgave 19 (20 punten)
Een van de rechthoekszijden van een rechthoekige driehoek heeft lengte 13. De lengten van de
anderen twee zijden zijn ook gehele getallen. Hoe lang zijn die zijden?
Opgave 20 (30 punten)
Acht mensen voeren een toneelstukje op. Sommigen spelen daarbij de rol van leugenaar, de anderen
van waarheidsspreker. Aan de toeschouwer de taak vast te stellen wie liegt en wie niet.
Anton zegt: minstens 1 van ons liegt.
Bettie zegt: minstens 2 van ons liegen.
Conny zegt: minstens 3 van ons liegen.
Diana zegt: Gerard is niet het oudst.
Erik zegt: minstens 5 van ons liegen.
Frans zegt: minstens 6 van ons liegen.
Gerard zegt: ik ben het jongst en Hannie is het oudst.
Hannie zegt: ik ben het oudst en Gerard is het jongst.
Wie spreekt de waarheid en wie liegt?
Opgave 21 (20 punten)
Hoeveel rijtjes van vier verschillende niet-negatieve gehele getallen zijn er die als som 10
hebben en 0 niet op de eerste plaats hebben?
Opgave 22 (30 punten)
Welk van de gehele getallen tussen 1 en 1000 heeft de meeste delers?
Opgave 23 (20 punten)
Noem alle natuurlijke getallen x tussen 100 en 1000 die aan de volgende eisen voldoen:
- x wordt met drie gelijke cijfers geschreven
- er is een natuurlijk getal n zo dat x = 1 + 2 + 3 + ... + n
Opgave 24 (20 punten)
Op de tekening staat het stratenplan van een kleine kazerne. Hoeveel
gesloten wegen zijn er die alle punten precies één keer aandoen?
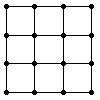 Met "gesloten weg" bedoelen we hier een weg die eindigt op het punt
waar hij begonnen is; hierbij letten we niet op het punt en ook niet op
de richting van de weg.
Met "gesloten weg" bedoelen we hier een weg die eindigt op het punt
waar hij begonnen is; hierbij letten we niet op het punt en ook niet op
de richting van de weg.
Opgave 25 (30 punten)
Van een rechthoekige driehoek is de lengte van de schuine zijde 25.
De straal van zijn ingeschreven cirkel is 3.
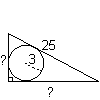 Hoelang zijn de andere twee zijden?
Hoelang zijn de andere twee zijden?
Opgave 26 (20 punten)
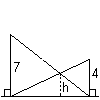 Bereken h
Bereken h
Opgave 27 (15 punten)
Wilma roeit stroomopwaarts. Twee uur lang van 12 tot 2. Dan keert zij om en roeit met
de stroom mee terug. Bij het keerpunt is haar hoed in het water gevallen. Wilma roeit
stug door. Die hoed komt wel achter haar aan. Om 3 uur is wilma terug bij de startlijn
(een denkbeeldige lijn dwars over de rivier waar zij om 12 uur begon te roeien). Enige
tijd later komt ook de hoed bij de startlijn aan. Hoe laat is het dan? (Neem aan dat
Wilma steeds even hard geroeid heeft, dus dat haar snelheid ten opzichte van het water
constant was.)
Opgave 28 (5 punten)
Arie, Bertus, Carel en Dirk worden verdacht van diefstal van een moterfiets. Bij het
verhoor leggen ze de volgende verklaringen af.
Arie: Ik ben onschuldig.
Bertus: Carel heeft het gedaan.
Carel: Bertus liegt.
Dirk: Bertus heeft het gedaan.
Drie van deze vier uitspraken zijn waar. Wie is de dief?
Opgave 29 (15 punten)
Van een rechthoekige tafel met vier even lange poten wordt van één van de poten een derde deel
afgezaagd. Van de poot die hier diagonaal tegenover staat wordt 11 cm afgezaagd. Van elk van de
resterende twee poten wordt 19 cm afgezaagd. De tafel blijkt hierna niet te wankelen. Hoe lang
waren de poten in het begin?
Opgave 30 (10 punten)
Tussen 10 en 11 uur is er een tijdstip waarop de grote en kleine wijzer van de klok precies
in dezelfde richting wijzen. Op dat tijdstip is het precies x minuten voor 11. Geeft het
getal x als een (niet vereenvoudigbare) breuk.
Opgave 31 (30 punten)
Het punt P ligt binnen de gelijkzijdige driehoek ABC zo dat PA = 3, PB = 4 en PC = 5.
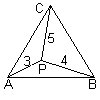 Bereken hoek APB.
Bereken hoek APB.
Opgave 32 (20 punten)
Merk de volgende punten in een kubus:
- de hoekpunten, acht stuks,
- de middens van de ribben, twaalf stuks,
- de middens van de zijvlakken, zes stuks,
- het middelpunt van de kubus.
Noem een drietal punten collineair als ze op één lijn liggen. Hoeveel collineaire drietallen
zijn er onder deze punten?
Opgave 33 (20 punten)
11 tot de macht 1992 wordt gedeeld door 100. Wat is de rest?
Opgave 34 (15 punten)
50! is het product van de natuulijke getallen 1 tot en met 50. Het is een getal van 65 cijfers.
Aan de rechterkant van dit getal staat een rijtje nullen.
Hoeveel nullen bevat dit rijtje?
Opgave 35 (10 punten)
Tussen 6 uur 's morgens en 6 uur 's avonds haalt de grote wijzer de kleine wijzer x keer in.
x = ?
Opgave 36 (30 punten)
Op tafel liggen zeven stuivers. Een van die stuivers wordt omringd door de andere zes.
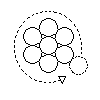 Een achtste stuiver rolt éénmaal om de figuur heen die door de zeven stuivers gevormd word.
Hoe vaak draait hij daarbij om zijn as?
Een achtste stuiver rolt éénmaal om de figuur heen die door de zeven stuivers gevormd word.
Hoe vaak draait hij daarbij om zijn as?
Opgave 37 (10 punten)
Een kleuter zit met een emmer water te spelen. Hij gooit de helft van
het water weg en voegt daarna een liter water toe. Dit herhaalt hij 2
keer en dat ziet er 2,5 liter water in. Hoeveel liter water zat er
oorspronkelijk in de emmer?
Opgave 38 (30 punten)
De knooppunten Vierbergen en Achtenaar worden gescheiden door een rechte
rivier die overal 700 meter breed is. De afstand van Vierbergen tot de rivier
is 400 meter en de afstand van Achtenaar tot de rivier is 500 meter. Hemelsbreed
is de afstand van Vierbergen to Achtenaar 2000 meter. Het rijk bouwt een brug
over de rivier die de rivier recht oversteekt en verbindt beide knooppunten
door middel van rechte wegen met de brug; het doet dat zo dat de afstand van
Vierbergen naar Achtenaar over de brug zo klein mogelijk is. Wat is die afstand?
</H3>
Tijdens een ruzie in de saloon tussen 7 cowboys werd er door elke cowboy 1 keer
geschoten. (Ze schoten na elkaar). Precies één cowboy overleefde de schietpartij.
Niemand schoot op zichzelf. Chris schoot Eddy neer. Al werd gedood door Freddy.
Al vermoordde Gerald. Bill schoot op Dave. Chris overleefde. Gerald schoot iemand
dood. Wie?
<HR>
<H3>Opgave 40 (20 punten)</H3>
Een paard staat op een schaakbord op het veldje linksonder (a1). Op hoeveel manieren
kan het met precies 7 paardesprongen in de rechterbovenhoek (h8) belanden?
<HR>
<H3>Opgave 41 (30 punten)</H3>
Een vierkant met zijde 10 wordt verdeeld in twee vierhoeken A en B. A heeft omtrek
28 en B heeft omtrek 34. Wat is de oppervlakte van vierhoek A?
<CENTER><IMG SRC = )
Opgave 42 (15 punten)
De spijkers staan in een zuivere roosteropstelling (op de snijpunten van een stel
horizontale en verticale lijnen met onderlinge afstand 1 cm). Door een elastiekje
om een aantal spijkers te spannen kun je een gebied afgrenzen. Twee van zulke gebieden
zijn hier getekend.
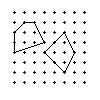 Deze gebieden hebben elk vier "binnenspijkers". Span een elastiekje zó, dat je vier
binnenspijkers krijgt, en bovendien de oppervlakte van het omspannen gebied zo klein
mogelijk is. Die minimale oppervlakte is ... cm.
Deze gebieden hebben elk vier "binnenspijkers". Span een elastiekje zó, dat je vier
binnenspijkers krijgt, en bovendien de oppervlakte van het omspannen gebied zo klein
mogelijk is. Die minimale oppervlakte is ... cm.
Opgave 43 (10 punten)
De vergelijking | | x-2 | -3 | = a heeft precies drie verschilende oplossingen. Wat is a?
Opgave 44 (15 punten)
Hoeveel getallen zijn er van negen cijfers waarin twee keer een 2, drie keer een 3 en vier keer
een 4 voorkomt?
Opgave 45 (10 punten)
Een zware balk wordt verplaatst met behulp van rollen die dwars onder de balk liggen. De diameter
van de rollen is 10cm. Wanneer de rollen ieder een volledige omwenteling gemaakt hebben, hoeveel
cm is de balk dan verplaatst?
Opgave 46 (30 punten)
Een gang die 2m breed en 3m hoog is maakt een haakse hoek. Een dunne onbuigzame staaf kan nog
net de hoek om in die gang. Wat is op zijn hoogst de lengte van die staaf?
Opgave 47 (15 punten)
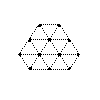
De twaalf punten in de tekening vormen een rooster van gelijkzijdige driehoeken. Hoeveel gelijkzijdige
driehoeken kun je tekenen in deze figuur (elk met drie van die twaalf punten als hoekpunten)?
Opgave 48 (15 punten)
Een grote vlaai heeft een doorsnede die anderhalf keer zo groot is als de doorsnede van een kleine
vlaai; ze zijn even dik. Die grote vlaai wordt verdeeld in stukken die elk even groot zijn als een
achtste deel van de kleine vlaai. In hoeveel stukken wordt de grote vlaai dan verdeeld?
Opgave 49 (20 punten)
Oslo en Lerwick (Shetland Eilanden) liggen beide op 60 graden noorderbreedte. Oslo ligt op 11 graden
oosterlengte en Lerwick op 1 graad westerlengte. Hoeveel kilometer is de afstand tussen deze plaatsen
gemeten langs de breedtecirkel? (Omtrek aarde: 40000 kilometer)
Opgave 50 (30 punten)
Vier positieve, reële getallen a, b, c, d worden met elkaar vermenigvuldigd. Vijf van de zes
mogelijke uitkomsten zijn 2, 3, 4, 5, 6. Wat is de zesde uitkomst?
Opgave 51 (10 punten)
Jan, Piet en Gerrit hebben samen 6 gulden. Degene met het meeste geld geeft 3 gulden aan degende
met het minste geld. Die dan het meeste geld heeft, geeft ook 3 gulden aan degene die dan het
minste geld heeft. Dan heeft Jan 1 gulden, Piet 2 gulden en Gerrit 3 gulden. Hoeveel had ieder
in het begin?
Opgave 52 (20 punten)
De getallen a en b zijn positief en geheel. 100 gedeeld door a geeft rest
1, 100 gedeeld door b geeft rest 2 en a gedeeld door b geeft rest 2. Wat
zijn a en b?
Opgave 53 (20 punten)
In een telefoongids staan de namen in alfabetische volgorde. Onder andere komen de namen Avezaath,
Baardewijk, Dijkstra, Ebbelink, Eckhard, Kwakkernaat, Lamer, Rijnders, Samson en Sanders voor. Tussen
"Baardewijk" en "Dijkstra" staan 102 namen. Tussen "Eckhard" en "Kwakkernaat" staan 211 namen. Tussen
"Lamers" en "Rijnders" staan 150 namen. Tussen "Avezaath" en "Sanders" staan 471 namen. Hoeveel namen
staan er tussen "Ebbelink" en "Samson"?
Opgave 54 (30 punten)
Bij het slot van een reünie neemt iedereen van iedereen afscheid. Daarbij geven een man en een vrouw
elkaar een hand en een zoen. Twee vrouwen geven elkaar alleen een zoen, en twee mannen geven elkaar
alleen een hand. In totaal wordt er 671 keer een zoen gegeven. Bepaal hoeveel keer er een hand gegeven
wordt, als verder gegeven is dat er meer vrouwen dan mannen zijn.
Opgave 55 (15 punten)
Hoeveel getallen zijn er tussen 1000 en 10000 die bestann uit twee gelijke oneven cijfers, een ander
oneven cijfer en een even cijfer? (Bijvoorbeeld 1990, 1989)
Opgave 56 (30 punten)
Het positieve gehele getal n is een drievoud. Verder is n!=1405006117752879898543142606244511569936384000000000
Welk getal is n dan?
Opgave 57 (40 punten)
In een vaas zitten witte en zwarte knikkers. Het aantal zwarte knikkers is tien groter dan het aantal witte.
Indien je zomaar twee knikkers gelijktijdig uit de vaas haalt is de kans dan je zowel een zwarte als een witte
hebt getrokken een half (50%). Hoeveel knikkers zitten er in de vaas?
Opgave 58 (20 punten)
Voor een uitwedstrijd gaan iets meer dan 2000 fans van een club in Utrecht naar Eindhoven met bussen.
Bij vertrek zitten in alle bussen evenveel fans. Onderweg krijgen twee bussen panne. De fans uit die
twee bussen worden over de andere bussen verdeeld: elke bus krijgt er precies drie fans bij. Met hoeveel
bussen vertrokken de fans uit Utrecht en hoeveel fans zaten er bij het vertrek in elke bus?
Opgave 59 (30 punten)
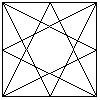
In een vierkant met zijde 1 verbindt men elk hoekpunt met de middens van de niet-aanliggende zijden.
Wat is de oppervlakte van de achthoek die zo ontstaat?
Opgave 60 (25 punten)
Gegeven zijn vier punten die niet in één vlak liggen. Hoveel vlakken zijn er die tot alle vier die punten
gelijke afstand hebben?
Opgave 61 (30 punten)
Twee punten A en B liggen op afstand 2,5 in een vlak. Rond punt A zijn zeven cirkels
getekend met A als middelpunt en stralen oplopend van 1 t/m 7. Evenzo zijn rond punt B
zeven cirkels getekend met stralen 1 t/m 7. Hoeveel snijpunten hebben deze cirkels met elkaar?
Opgave 62 (20 punten)
Peter loopt over een rechte weg. Rechts van hem staat een telegraafpaal, precies 130 meter van hem
verwijderd. Hij loopt 100 meter verder, dan is de telegraafpaal weer precies 130 meter van hem af. Hij
loopt nog eens 110 meter verder. Hoe ver is die paal nu van hem verwijderd?
Opgave 63 (30 punten)
Een cirkel raakt alle zijden van een vierhoek. De zijden hebben achtereenvolgens als lengten: 9, 7, 12, x
(zie plaatje). Bereken x.
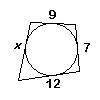
Opgave 64 (15 punten)
Hoeveel verschillende puzzelstukjes zijn er te maken uit vijf congruente gelijkzijdige driehoekjes
die langs gehele zijden tegen elkaar moeten liggen? (Stukjes die door draaiing of spiegeling in elkaar
kunnen overgaan, worden als gelijk beschouwd.) Een voorbeeld zie je hieronder.
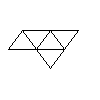
Bronvermelding:
- Nederlandse Wiskunde Olympiade
- Katholieke Universiteit Nijmegen



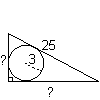


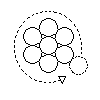
</H3>
Tijdens een ruzie in de saloon tussen 7 cowboys werd er door elke cowboy 1 keer
geschoten. (Ze schoten na elkaar). Precies één cowboy overleefde de schietpartij.
Niemand schoot op zichzelf. Chris schoot Eddy neer. Al werd gedood door Freddy.
Al vermoordde Gerald. Bill schoot op Dave. Chris overleefde. Gerald schoot iemand
dood. Wie?
<HR>
<H3>Opgave 40 (20 punten)</H3>
Een paard staat op een schaakbord op het veldje linksonder (a1). Op hoeveel manieren
kan het met precies 7 paardesprongen in de rechterbovenhoek (h8) belanden?
<HR>
<H3>Opgave 41 (30 punten)</H3>
Een vierkant met zijde 10 wordt verdeeld in twee vierhoeken A en B. A heeft omtrek
28 en B heeft omtrek 34. Wat is de oppervlakte van vierhoek A?
<CENTER><IMG SRC = )