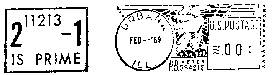After the
23rd Mersenne prime was found at the University of Illinois, the mathematics
department was so proud that they had their postage meter changed to stamp
"2^11213-1 is prime" on each envelope.
1. Early History
Many early writers felt that the numbers of the form 2^n-1 were prime for
all primes n, but in 1536 Hudalricus
Regius showed that 2^11-1 = 2047 was not prime (it is 23*89). By 1603 Pietro
Cataldi had correctly verified that 2^17-1 and 2^19-1 were both prime, but then
incorrectly stated 2^n-1 was also prime for 23, 29, 31 and 37. In 1640 Fermat
showed Cataldi was wrong about 23 and 37; then Euler
in 1738 showed Cataldi was also wrong about 29.
Sometime later Euler showed Cataldi's assertion
about 31 was correct.
Enter French monk Marin Mersenne (1588-1648). Mersenne stated in the preface to his Cogitata Physica-Mathematica (1644) that the numbers 2^n-1 were prime for
n = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127 and 257and were composite for all other positive integers n < 257. Mersenne's (incorrect) conjecture fared only slightly better than Regius', but still got his name attached to these numbers.
Definition: When 2^n-1 is prime it is said to be a Mersenne prime.It was obvious to Mersenne's peers that he could not have tested all of these numbers (in fact he admitted as much), but they could not test them either. It was not until over 100 years later, in 1750, that Euler verified the next number on Mersenne's and Regius' lists, 2^31-1, was prime. After another century, in 1876, Lucas verified 2^127-1 was also prime. Seven years later Pervouchine showed 2^61-1 was prime, so Mersenne had missed this one. In the early 1900's Powers showed that Mersenne had also missed the primes 2^89-1 and 2^107-1. Finally, by 1947 Mersenne's range, n < 258, had been completely checked and it was determined that the correct list is:
n = 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107 and 127.See the table of known Mersenne primes below.
Definition: A positive integer n is called a perfect number if it is equal to the sum of all of its positive divisors, excluding n itself.For example, 6 is the first perfect number because 6=1+2+3. The next is 28=1+2+4+7+14. The next two are 496 and 8128. These four were all known before the time of Christ. Look at these numbers in the following partially factored form:
2*3, 4*7, 16*31, 64*127.Do you notice they all have the same form 2^(n-1)*(2^n-1) (for n = 2, 3, 5, and 7 respectively)? And that in each case 2^n-1 was a Mersenne prime? In fact it is easy to show the following theorems:
Theorem One: k is an even perfect number if and only if it has the form 2^(n-1)*(2^n-1) and 2^n-1 is prime.So the search for Mersennes is also the search for even perfect numbers! (The proof of these theorem can be found in almost any text on elementary number theory, for example Burton80.)Theorem Two: If 2^n-1 is prime, then so is n.
You may have also noticed that the perfect numbers listed above (6, 28, 496, 8128) all end with either the digit 6 or the digit 8--this is also very easy to prove (but no, they do not continue to alternate 6, 8, 6, 8,...). If you like that digit pattern, look at the first four perfect numbers in binary:
(The binary digit pattern is a consequence of Theorem One.)110 11100 111110000 1111111000000
Finally, it is not known whether or not there is an odd
perfect number, but if there is one it is big!
3. Table of Known Mersenne Primes
Let M(p) = 2^p-1 and P(p) = 2^(p-1)(2^p-1).
The list of all known primes p for which M(p) is a Mersenne
prime (therefore P(p) is a perfect number) follows:
p digits digits year discoverer
in M(p) in P(p) found
1 2 1 1 ---- ----
2 3 1 2 ---- ----
3 5 2 3 ---- ----
4 7 3 4 ---- ----
5 13 4 8 1456 anonymous
6 17 6 10 1588 Cataldi
7 19 6 12 1588 Cataldi
8 31 10 19 1772 Euler
9 61 19 37 1883 Pervushin
10 89 27 54 1911 Powers
11 107 33 65 1914 Powers (note 1)
12 127 39 77 1876 Lucas
13 521 157 314 1952 Robinson
14 607 183 366 1952 Robinson
15 1279 386 770 1952 Robinson
16 2203 664 1327 1952 Robinson
17 2281 687 1373 1952 Robinson
18 3217 969 1937 1957 Riesel
19 4253 1281 2561 1961 Hurwitz
20 4423 1332 2663 1961 Hurwitz
21 9689 2917 5834 1963 Gillies
22 9941 2993 5985 1963 Gillies
23 11213 3376 6751 1963 Gillies
24 19937 6002 12003 1971 Tuckerman
25 21701 6533 13066 1978 Noll & Nickel
26 23209 6987 13973 1979 Noll
27 44497 13395 26790 1979 Nelson & Slowinski
28 86243 25962 51924 1982 Slowinski
29 110503 33265 66530 1988 Colquitt & Welsh
30 132049 39751 79502 1983 Slowinski
31 216091 65050 130100 1985 Slowinski
?? 756839 227832 455663 1992 Slowinski & Gage
?? 859433 258716 517430 1994 Slowinski & Gage
Lucas-Lehmer Test: For p odd, the Mersenne number 2^p-1 is prime if and only if 2^p-1 divides S(p-1) where S(n+1) = S(n)^2-2, and S(1) = 4.(It is also possible to start with S(1)=10 and certain other values depending on p.) In pseudocode this test is:
Lucas_Lehmer_Test(p):
s := 4;
for i from 3 to p do s := s^2-2 mod 2^p-1;
if s == 0 then
2^p-1 is prime
else
2^p-1 is composite;
In 1811 Peter Barlow wrote in his text Theory of Numbers that 2^30*(2^31-1) "is the greatest [perfect number] that will be discovered; for as they are merely curious, without being useful, it is not likely that many person will attempt to find one beyond it." I wonder what he would have made of the first attempts to climb Mount Everest, to run faster miles, or to jump a longer broad jump--other tasks that are curious but not useful. Obviously no one in the late 1800's had any idea of the power of modern computers. What might we know about the machines of 50 years from now?
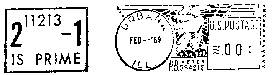After the
23rd Mersenne prime was found at the University of Illinois, the mathematics
department was so proud that they had their postage meter changed to stamp
"2^11213-1 is prime" on each envelope.
The 25th and 26th Mersenne primes were found by high-school students Laura Nickel and Curt Noll, who, though they had no understanding of the mathematics involved, used Lucas' simple test on the local university's mainframe (CSUH's CDC 720) to find the next two primes. Their discovery of the first prime made the national television news and the front page of the New York times. They went their separate ways after finding the first prime, but Noll kept the program running to find the second--so Noll claims complete ownership. Noll searched later, and though he never found another Mersenne prime, he is one of a team that holds the record for the largest non-Mersenne prime. He currently works for Silicon Graphics.
Slowinski, who works for Cray computers, has written a version of the Lucas test
that he has convinced many Cray labs around the world to run in their spare time
(time that would be lost otherwise). He had to delay announcing one of his prime
records until he got permission to begin looking for it. Slowinski's search for
record primes is "not so organized as you would suppose" (his words), as he does
not search systematically. In fact, looking at the table of Mersennes you see he
missed the 29th prime but found the 30th and 31st. Colquitt & Welsh worked to fill
in the gaps and found the 29th. Most of the range between the largest and second
largest prime has not been searched, and will not be for some time. At the current
speed of computers the time to test the tens of thousands of numbers between the
three largest is almost beyond our reach, but you can help by joining the GREAT
Internet Mersenne Prime Search.
5. Conjectures and Unsolved Problems
If k>1 and p=4k+3 is prime, then 2p+1 is prime if and only if 2^p = 1 (mod 2p+1).So if p=4k+3 and 2p+1 are prime then the Mersenne number 2^p-1 is composite (and it seems reasonable to conjecture that there are infinitely many primes pairs such p, 2p+1).
Let p be any odd natural number. If two of the following conditions hold, then so does the third:
- p = 2^k+/-1 or p = 4^k+/-3
- 2^p-1 is a prime (obviously a Mersenne prime)
- (2^p+1)/3 is a prime.
It seems very unlikely that they would all be prime and this is no doubt another example of Guy's strong law of small numbers [Guy94].C1 = 3 C2 = 7 C3 = 127 C4 = 170141183460469231731687303715884105727 C5 > 10^51217599719369681879879723386331576246