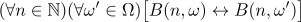In two words, Ω-invariance is a new notion of (Turing) computability based on infinitesimals.  With some extra effort, Ω-invariance can even capture the constructive notion of algorithm in the sense of Errett Bishop’s Constructive Analysis.

In more detail, Ω-invariance is defined as follows: 

Essentially, every version of Nonstandard Analysis includes a set ℕ, the set of natural/standard/finite numbers, and its extension *ℕ, the set of hypernatural numbers.  The set Ω = *ℕ \ ℕ  is the set of infinite/nonstandard numbers.  Now let B(n,m) ∈ ∆0 be a standard formula with two free variables as shown and fix an infinite number ω.  Then B(n,ω) is Ω-invariant if

Intuitively, a formula is Ω-invariant if it is independent of the choice of the infinite number (or equivalently: infinitesimal) in its definition. 

It is easy to show that Ω-CA, i.e. comprehension for Ω-invariant formulas, implies ∆1-CA, i.e. compre-hension for Turing computable sets.  With more effort, one can show that Ω-CA can be added con-servatively to a nonstandard version of RCA0.  In other words, the Ω-invariant sets are exactly the Turing computable sets (in a technical sense). 

On a philosophical note, when infinitesimals are used in Physics, Engineering, etc, the choice of the particular infinitesimal is always irrelevant, especially if the results describe physical reality.  In this sense, results in the mathematical practice of Physics are Ω-invariant and therefore computable.

To capture Errett Bishop’s ‘constructive’ notion of algorithm, we need to limit the class of Ω-invariant objects somehow.  As it turns out, the right way to do this is to consider only formulas A which satisfy (a version of) the Transfer Principle  A ⟷ *A, where ‘*’ is the star morphism of NSA.  Some preliminary results can be found here.  Thus, in the same way as Constructive Analysis is limited to formulas that come with proofs, we only consider formulas A which satisfy (a version of) the Transfer Principle  A ⟷ *A. 

The above yields a new interpretation of Constructive Analysis (aka BISH) inside a certain system ℕSA of Nonstandard Analysis with the following properties:

(i) Non-constructive principles (LPO, LLPO, MP, etc) are interpreted as instances of the Transfer Principle from Nonstandard Analysis, which are not available in the system ℕSA.  This even seems to hold for the semi-constructive WMP (Weak Markov's Principle) and BD-N.

(ii) Non-constructive principles still satisfy the well-known equivalences and implications of Constructive Reverse Mathematics under the interpretation.    

(iii) Due to the absence of Markov's principle, the primitive notion of algorithm on ℕ is weaker than that of recursive function in BISH, i.e. not all ∆1-formulas are decidable.  This property is preserved by our interpretation. 

If your are interested, I can email you the recently submitted paper documenting these results.  As Per Martin-Löf intended his Type Theory as a foundation for BISH, it seems worthwhile exploring the role of Ω-invariance there.