The Golden Section
The Golden Triangle
The Regular Pentagon and the Pentagram
The Dodecahedron
On this page we will derive some relations between a fundamental number and two famous geometrical
figures, the one planar, the other spatial. As a result we will understand how a regular dodecahedron can be constructed
starting from a cube by putting suitable "roofs" on it, as Euclid already did...
The Golden Section

The starting point is the division of a line segment in mean and extreme ratio.
A point on a line segment divides this segment in mean and extreme ratio if the ratio of the
whole segment to one part is the same as the ratio of that part to the remaining part of the line segment.
Given a line segment AB, the point P divides AB in mean and extreme ratio if
$$\frac{AB}{AP}=\frac{AP}{PB}$$
This division of the line segment is called the golden section.
The ratio AB/AP is called the golden ratio and often represented by $\varPhi$.
For the construction of the point P on the line segment AB it's more adequate to use the inverse ratio
$$\varphi = \dfrac{1}{\varPhi} = \dfrac{AP}{AB}$$
Calculation of $\varphi$
$$\frac{AB}{AP} = \frac{AP}{PB}$$
$$\frac{AP}{AB}=\frac{PB}{AP}$$
$$\frac{AP}{AB}=\frac{AB-AP}{AP}$$
$$\frac{AP}{AB}=\frac{1-\frac{AP}{AB}}{\frac{AP}{AB}}$$
$$\varphi=\frac{1-\varphi}{\varphi}$$
$$\varphi^2+\varphi-1=0$$
As $\varphi\gt0$, $\varphi$ is the positive solution of this quadratic equation
$$\varphi=\frac{\sqrt{5}-1}{2} \approx{0.618}$$
It follows that the golden ratio $\varPhi = \dfrac{1}{\varphi} = \dfrac{3-\sqrt{5}}{2} \approx{1.618}$.
From $\varphi^2+\varphi-1=0$ we derive that $1+\varPhi-\varPhi^2=0$.
Another interesting relation between $\varphi$ and $\varPhi$ is $\varPhi -\varphi=1$.
As $\varphi^2=1-\varphi$ it follows that all entire powers of $\varphi$ can be expressed as $m \varphi +n$, where $m$ and $n$ are entire numbers. The same property holds for $\varPhi$ .
Construction of the golden section

The classical construction of the golden section looks rather easy. Given the segment $AB$ we construct $BC$ with length $\dfrac{AB}{2}$ perpendicular to $AB$.
Then $$AC=\sqrt{AB^2+BC^2}=\dfrac{AB}{2} \sqrt{5}$$
$$AP = AD = AB \dfrac{\sqrt{5}-1}{2}$$
Starting with the line segment $AB$ the whole construction needs some more steps: the construction of $BC$ perpendicular to $AB$, the point $C$ such that the length of $BC$ is half the length of $AB$.

A special isosceles triangle or "golden triangle"

We consider an isosceles triangle with a top angle measuring 36 degrees. Both base angles then measure 72 degrees.
BD is the bisector of the angle in B.
From the fact that the triangles ABD and BDC are isosceles triangles it follows that
BC=BD=AD.
Moreover the triangles BDC and ABC are similar triangles. It follows that
AC/BD = BC/DC or AC/AD = AD/DC,
which means that in the original triangle the base BC equals the greatest part of the side AC divided by the
golden section!
If we consider the circle with centre A and radius r = AB, then BC is a side s10 of the regular decagon that is inscribed in
the given circle.

A property of the regular pentagon

Considering a regular pentagon with two non-intersecting diagonals and taking into account what we already derived above, it
follows that the length of the side equals the greatest part of the diagonal divided by the golden section.

The pentagram
The five diagonals of a regular pentagon define a star-shaped figure that is called
a pentagram . It has five sides and five vertices.
The interior intersections of the sides aren't vertices of the pentagram.
A pentagram is an example of a non-convex polygon. A polygon is convex if and
only if any line containing a side of the polygon doesn't contain a point in the interior of the polygon.
As a triangle always is convex and there don't exist non-convex regular polygons with four sides, the pentagram, in this
sense is the simplest of the non-convex regular polygons.
From the relation between the sides and the diagonals of a regular pentagon and considering the the second figure above, one
easily states that two non-consecutive sides of a pentagram divide each other in mean and extreme ratio!
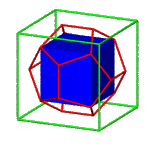
Construction of a regular dodecahedron
Starting with a cube we can construct a regular dodecahedron by putting appropriate "roofs" on each face of the cube.
This is the method used by Euclid (book XIII proposition 17). The bases of the roofs are the faces of the cube and
all edges of the roofs that aren't edges of the cube must have the same length.
Moreover the adjacent faces of two meeting roofs must form a regular planar pentagon. The length of the
diagonals of the pentagons equals the length of the sides of the cube. It follows that the length of the edges of
the dodecahedron is the greatest of the two parts in which the edge of the cube is divided by the golden section!
The height of the roofs equals half the side of the pentagons.
As easily can be derived from a frontal view,
the angles between the base and a triangular face and between the base and a trapeziodal face of the roof are
complementary. It follows that the pentagons are planar.
A cube-to-dodecahedron transformation
Bob Faulkner informed me via email from the USA how he had constructed a material model to illustrate a nice
cube-to-dodecahedron transformation. Complimenting me on my own displays, he asked if I might realize his material model
as a computer animation. I accomplished the animation by following Euclid's method: first defining six roofs upon a given
cube, then completing the roofs by including their square bases. In this way, the original cube could be omitted.
Next, choosing one of the roofs as fixed, the four adjacent roofs were hinged along their edges common with the fixed roof.
The sixth roof was then hinged to one of its already hinged neighbours. Finally, it's possible to unfold the
dodecahedron and refold it into the cube that served as the basis for its construction.
Following Bob's idea, I prepared an endless computer animation to illustrate this very nice relation between the cube
and the dodecahedron that's constructed upon it.

return to the homepage
Send an e-mail
Last update: November 2025.