Although Euclid (book XIII proposition 16) constructs a regular icosahedron starting with a given sphere, there's a nice method to construct a regular icosahedron starting from a given cube.

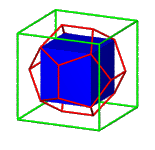
We want six of the edges of the icosahedron to be positioned in the faces of the given cube as indicated on the first drawing. The twelve vertices of the icosahedron must be the endpoints of this line segments (second drawing)!
We should derive the length of the edges as a function of the length of the edges of the given cube, or even better, their proportion (third drawing).

The so-called Book XIV of the "Elements"

It is known that the so-called books XIV and XV of the "Elements" are not by Euclid. Book XIV is the work of Hypsicles, who probably lived in the second half of the second century B.C. This book deals with the comparison of different regular polyhedra.

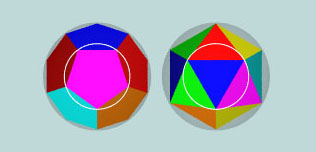
A very interesting property about the regular icosahedron and dodecahedron inscribed in the same sphere is expressed in proposition 2:

The same circle circumscribes both the pentagon of the dodecahedron and the triangle of the icosahedron inscribed in the same sphere.

From this proposition it follows that the dodecahedron an isosahedron inscribed in the same sphere also share their inscribed sphere. As a consequence we obtain the following nice property of those polyhedra: the ratio of their volumes is the same as the ratio of their surfaces.

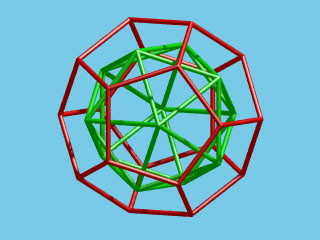
The centers of the faces of a regular dodecahedron are the vertices of a regular icosahedron and the centers of the faces of a regular icosahedron are the vertices of a regular dodecahedron.
Both regular polyhedra are "dual polyhedra".

return to the homepage