THE QUADRATRIX
Trisecting an angle - Squaring the circle

Introduction

Three famous geometrical construction problems, originating from ancient Greek mathematics occupied many mathematicians until modern times. These problems are

In the ancient Greek tradition the only tools that are available for these constructions are a ruler and a compass. During the 19th century the French mathematician Pierre Wantzel proved that under these circumstances the first two of those constructions are impossible and for the squaring of the circle it lasted until 1882 before a proof had been given by Ferdinand von Lindemann!
If we extend the range of tools the problems can be solved. New tools can be material tools (ex. a "marked ruler", that's a ruler with two marks on it, a "double ruler", that's a ruler with two parallel sides,...), or mathematical tools (ex. special curves as conics, spirals,...).

The quadratrix

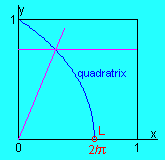
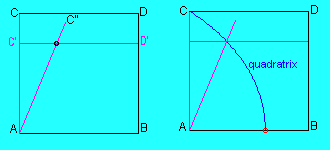
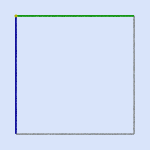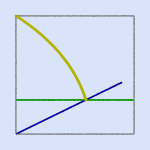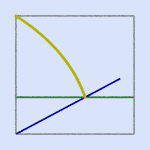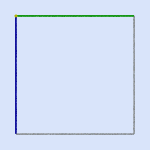
The quadratrix (of Hippias) is one of the curves that can be used to solve the problem of the trisection of an angle and in some sense the squaring of the circle. The curve already appears in ancient Greek geometry. It's named after Hippias of Elis and was used by Dinostratus and Nicomedes.

The curve is defined in a "dynamical" way. Consider the square ABDC. Suppose that AC rotates uniformly about A until it coincides with AB and that in the same time CD descends uniformly to AB. So AC and CD reach their final position AB at the same time. The quadratrix is the locus of the intersection points of both moving line segments.

This definition of the curve suggests that it isn't very difficult to construct a mechanical tool to obtain a drawing of a quadratrix. The quadratrix has a starting point but no end point! Indeed, when both moving segments reach their final position there is no longer an intersection point. However we see that there should exist a limit point L. Using a coordinate system with A in the origin, B(1,0), C(0,1) and D(1,1) we obtain the following equation for the quadratrix:

x = y cot (y*pi/2)
This expression doesn't have any sense for y = 0. The limit for x as y approaches 0 is 2/pi.

The trisection of an angle using the quadratrix

First we consider a special case with historical importance. It is possible to construct an angle of 60 degrees using only ruler and compass, but it has been proved that it's impossible to construct an angle of 20 degrees using only the same tools. We will show how the construction is done using the quadratrix.

Starting with the constructed angle of 60 degrees, we obtain the points P and Q. The point R is determined in such a way that AQ = 3 AR. This leads to the point S on the quadratrix. From the definition of the quadratrix it follows immediately that the angle BAS measures 20 degrees.
Squaring the circle using the quadratrix

Although in the history of mathematics the quadratrix has been played a role in solving this classical problem, it's usefulness is of another nature than in the case of the trisection of an angle. In fact one has to admit the existence of the limit point L that can't be reached by the dynamical process that defines the quadratrix.
Once we admit that we can use the limit point L, only ruler and compass are needed for the further construction of the square with side length sqrt(pi). The area of this square equals the area of the circle with radius OR.

If we choose the radius OR of the given circle as the unit to measure line segments, then we have to construct a line segment with length sqrt(pi). We already know that the length of OL is 2/pi. If OM = ML then we already have constructed a line segment with length 1/pi.
The construction on the right where AC=1, CD=1/pi, CE=1 and BE//AD leads to the point B and to the line segment BC with length pi. Using a further well known construction we obtain the line segment CF with length sqrt(pi).
All these constructions are possible using only ruler and compass! The area of the square constructed on CF equals the area of the circle with radius OR!

Herman Serras, March 2001
return to the homepage