15th BALKAN MATHEMATICAL OLYMPIAD
NICOSIA, CYPRUS, 1998
Problem 1
Find the number of different terms of the finite sequence
[k2/1998], where k = 1, 2,... , 1997 and
[x] denotes the integer part of x.
Problem 2
If n>= 2 is an integer and 0 < a1 <
a2 ... < a2n+1
are real numbers, prove the inequality:
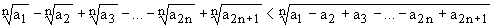
Problem 3
Let S be the set of all points inside and on the border of the
triangle ABC without one inside point T. Prove that S
can be represented as a union of closed segments no two of which have a
point in common. (A closed segment contains both of its ends.)
Problem 4
Prove that the equation y2 = x5 - 4
has no integer solutions.